Javascript required
Skip to content Skip to sidebar Skip to footer
Home / Given a Continuous Uniform Distribution Show That a μ a b 2 and B σ2 B−a 2 12

Given a Continuous Uniform Distribution Show That a μ a b 2 and B σ2 B−a 2 12

Probability is one of the basics of mathematics. It is the probability distribution that represents equally likely outcomes i.e. the probability of each occurring is the same. There are two types of uniform distribution: Discrete uniform distribution and continuous uniform distribution (the most common type in elementary statistics). It defines the density function of the random variable, mean, and variance.

Uniform Distribution

A uniform distribution is a distribution that has constant probability due to equally likely occurring events. It is also known as rectangular distribution (continuous uniform distribution). It has two parameters a and b: a = minimum and b = maximum. The distribution is written as U(a, b). Types of uniform distribution are:

  1. Continuous Uniform Distribution: A continuous uniform probability distribution is a distribution that has an infinite number of values defined in a specified range. It has a rectangular-shaped graph so-called rectangular distribution. It works on the values which are continuous in nature. Example: Random number generator
  2. Discrete Uniform Distribution: A discrete uniform probability distribution is a distribution that has a finite number of values defined in a specified range. Its graph contains various vertical lines for each finite value. It works on values that are discrete in nature. Example: A dice is rolled.

Graph of Uniform Distribution:

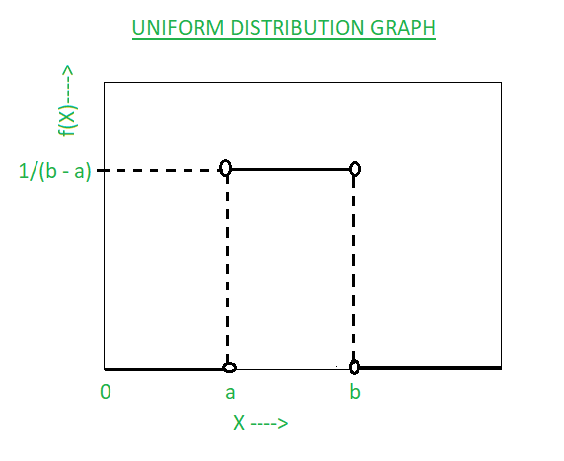
Calculating the height of the rectangle:

The maximum probability of the variable X is 1 so the total area of the rectangle must be 1.

Area of rectangle = base * height = 1

(b – a) * f(x) = 1

f(x) = 1/(b – a) = height of the rectangle

Note: Discrete uniform distribution: Px = 1/n. Where, Px = Probability of a discrete variable, n = Number of values in the range

Uniform Distribution Formula

A random variable X is said to be uniformly distributed over the interval -∞ < a < b < ∞. Formulae for uniform distribution:

Probability density function(pdf)  f(x) = 1/( b – a), a ≤ x ≤ b
Mean(μ)

\int_{a}^{b} x.f(x) \,dx =\frac{1}{b-a}[\frac{x^2}{2}]_a^b

 = (a + b)/2
Variance (σ2 )

\int_{a}^{b} x.f(x) \,dx =\frac{1}{b-a}[\frac{x^2}{2}]_a^b

= μ2' – μ2 =\int_{a}^{b}x^2.\frac{1}{b-a}dx \hspace{0.1cm}-(\frac{a+b}{2})^2

= (b – a)2 /12
Standard Deviation (σ) = (b – a)/√12
Cumulative Distribution function (cdf) = (x – a)/(b – a) for x ∈ [a , b]
Median = (a + b)/2
For the conditional probability = P( c < x < d )

= (d – c ) * f(x)

= (d – c)/(b – a)

Sample Questions

Question 1: A random variable X has a uniform distribution over(-2, 2),

(i) find k for which P(X>k) = 1/2      (ii) Evaluate P(X<1)      (iii) P[|X-1|<1]

Solution:

(i) X =f(x) = 1/(b-a) =1/(2-(-2)) = 1/4

P(X>k) = 1 – P(X≤ k) = 1 –\int_{-2}^{k}f(x)dx

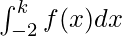
= 1 – (1/4).\int_{-2}^{k}dx  =1 – (k+2)/4 = 1/2

By solving we get k = 0

(ii) P(X<1) =\int_{-2}^{1}f(x)dx  =(1/4).\int_{-2}^{k}dx = 3/4

(iii) P[|X -1| <1] = P[1-1<X<1+1] = P[0 < x < 2] =\int_{0}^{1}f(x)dx = (1/4).\int_{0}^{1}dx  = 1/4

Question 2: If X is uniformly distributed in (-1 , 4) then

(i) its mean is ______________.

(ii) its variance is ______________.

(iii) its standard deviation is ___________.

(iv) its median is ______________.

Solution:

Here, a = -1 and b = 4

(i) Mean (μ) = (4-1)/2 = 1.5

(ii) Variance(σ2) = (4+1)2 /12 = 2.08

(iii) Standard deviation(σ) =√2.08 = 1.443

(iv) Median = (4-1)/2 = 1.5

Question 3: If there are 52 cards in the traditional deck of cards with four suits: hearts, spade, clubs, and diamonds. Each suite contains 13 cards of which 3 cards are face cards. The new deck is formed by excluding the number of cards. Then what is the probability of getting a heart card from the modified deck?

Solution:

In the question, the given number of cards is finite so it is a discrete uniform distribution.

Formula for the probability in discrete uniform distribution is P(X) = 1/n

Probability of getting heart in the modified deck = 1/4 = 0.25

Question 4: Using the uniform distribution probability density function for random variable X, in (0, 20), find P(3< X < 16).

Solution:

Here, a = 0, b =20

f(x) = 1/(20 – 0) = 1/20

P(3< X < 16) = (16 – 3) * (1/20) = 13/20

Question 5: A random variable X has a uniform distribution over (-5 , 6), find cumulative distribution function for x = 3.

Solution:

Here, a = -5, b = 6, x = 3

CDF = (3 – (-5))/(6 – (-5)) = 8/11


cheeketreas1959.blogspot.com

Source: https://www.geeksforgeeks.org/uniform-distribution-formula/